链表环的入口数学原理

看一张简图。（图侵删）

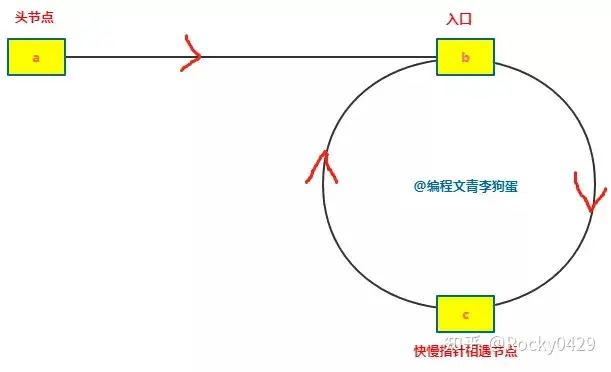
假设：

• 从头节点到入口的距离为 ab。
• 从入口到相遇点的距离为 bc。
• 从相遇点到入口的距离为 cb。

则链表环的长度 = bc + cb。

那么快慢指针相遇时所走过的步数为：

fast_step = ab + bc + n * (bc + cb) 【公式 1】

slow_step = ab + bc 【公式 2】

n 指的是 fast 指针走过的圈数，n 的取值肯定是 n ≥ 1，因为快指针 fast 最少要多跑一圈才能追上慢指针 slow。

又由于快指针每次走 2 步，慢指针每次走 1 步，所以又有：

fast_step = 2 * slow_step 【公式 3】

综合公式 1、公式 2、公式 3，得出：

ab + bc + n * (bc + cb) = 2 * (ab + bc) 【公式 4】

整理得：

ab = (n - 1) * (bc + cb) + cb 【公式 5】

其中 (n - 1) * (bc + cb) 正好是 (n - 1) 个环形的长度。

为了更好的理解公式 5，我们假设 n = 1，也就是快指针 fast 指针走一圈就可以碰到慢指针 slow。

那么公式 5 变成：

ab = cb

ab 是从节点到入口的距离，cb 是从相遇节点到入口的距离，这说明什么呢？

说明同时从头节点和相遇节点出发的两个指针，每次走 1 步，最终会在入口处相遇。

所以如果判断链表是环形链表，“找入口”就成了，在找到快慢指针相遇节点时，设置两个新节点 flag1 和 flag2。

其中 flag1 指向头节点，flag2 指向快慢指针相遇节点，然后每次移动 1 步，直至 flag1 和 flag2 相遇。

Code

public ListNode EntryNodeOfLoop(ListNode pHead)
{
    if(pHead == null || pHead.next == null){
        return null;
    }

    ListNode fast = pHead;
    ListNode slow = pHead;

    while(fast != null && fast.next != null){
        fast = fast.next.next;
        slow = slow.next;
        if(fast == slow){
            ListNode slow2 = pHead;
            while(slow2 != slow){
                slow2 = slow2.next;
                slow = slow.next;
            }
            return slow2;
        }
    }
    return null;

}